Rare Events Logistic Regression (ReLogit)
2017-10-29
Built using Zelig version 5.1.4.90000
Rare Events Logistic Regression for Dichotomous Dependent Variables with relogit.
The relogit procedure estimates the same model as standard logistic regression (appropriate when you have a dichotomous dependent variable and a set of explanatory variables; see ), but the estimates are corrected for the bias that occurs when the sample is small or the observed events are rare (i.e., if the dependent variable has many more 1s than 0s or the reverse). The relogit procedure also optionally uses prior correction for case-control sampling designs.
Arguments
The relogit procedure supports four optional arguments in addition to the standard arguments for zelig(). You may additionally use:
tau: a vector containing either one or two values for \(\tau\), the true population fraction of ones. Use, for example, tau = c(0.05, 0.1) to specify that the lower bound on tau is 0.05 and the upper bound is 0.1. If left unspecified, only finite-sample bias correction is performed, not case-control correction.
case.control: if tau is specified, choose a method to correct for case-control sampling design: “prior” (default) or “weighting”.
bias.correct: a logical value of TRUE (default) or FALSE indicating whether the intercept should be corrected for finite sample (rare events) bias.
Note that if tau = NULL, bias.correct = FALSE, the relogit procedure performs a standard logistic regression without any correction.
Example 1: One Tau with Prior Correction and Bias Correction
Due to memory and space considerations, the data used here are a sample drawn from the full data set used in King and Zeng, 2001, The proportion of militarized interstate conflicts to the absence of disputes is \(\tau = 1,042 / 303,772 \approx 0.00343\). To estimate the model,
data(mid)z.out1 <- zelig(conflict ~ major + contig + power + maxdem + mindem + years,
data = mid, model = "relogit", tau = 1042/303772)## How to cite this model in Zelig:
## Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau. 2017.
## relogit: Rare Events Logistic Regression for Dichotomous Dependent Variables
## in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
## "Zelig: Everyone's Statistical Software," http://zeligproject.org/Summarize the model output:
summary(z.out1)## Model:
##
## Call:
## z5$zelig(formula = conflict ~ major + contig + power + maxdem +
## mindem + years, tau = 1042/303772, data = mid)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.0596 -0.0376 -0.0231 2.1085 4.4649
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -7.525688 0.179685 -41.883 < 2e-16
## major 2.433432 0.157561 15.444 < 2e-16
## contig 4.112491 0.157650 26.086 < 2e-16
## power 1.053747 0.217243 4.851 1.23e-06
## maxdem 0.048431 0.010065 4.812 1.50e-06
## mindem -0.065249 0.012802 -5.097 3.45e-07
## years -0.063359 0.005705 -11.106 < 2e-16
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 3979.5 on 3125 degrees of freedom
## Residual deviance: 1868.5 on 3119 degrees of freedom
## AIC: 1882.5
##
## Number of Fisher Scoring iterations: 6
##
## Next step: Use 'setx' methodSet the explanatory variables to their means:
x.out1 <- setx(z.out1)Simulate quantities of interest:
s.out1 <- sim(z.out1, x = x.out1)
summary(s.out1)##
## sim x :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## [1,] 0.002364324 0.0001550274 0.002359333 0.002093318 0.002679686
## pv
## 0 1
## [1,] 0.996 0.004plot(s.out1)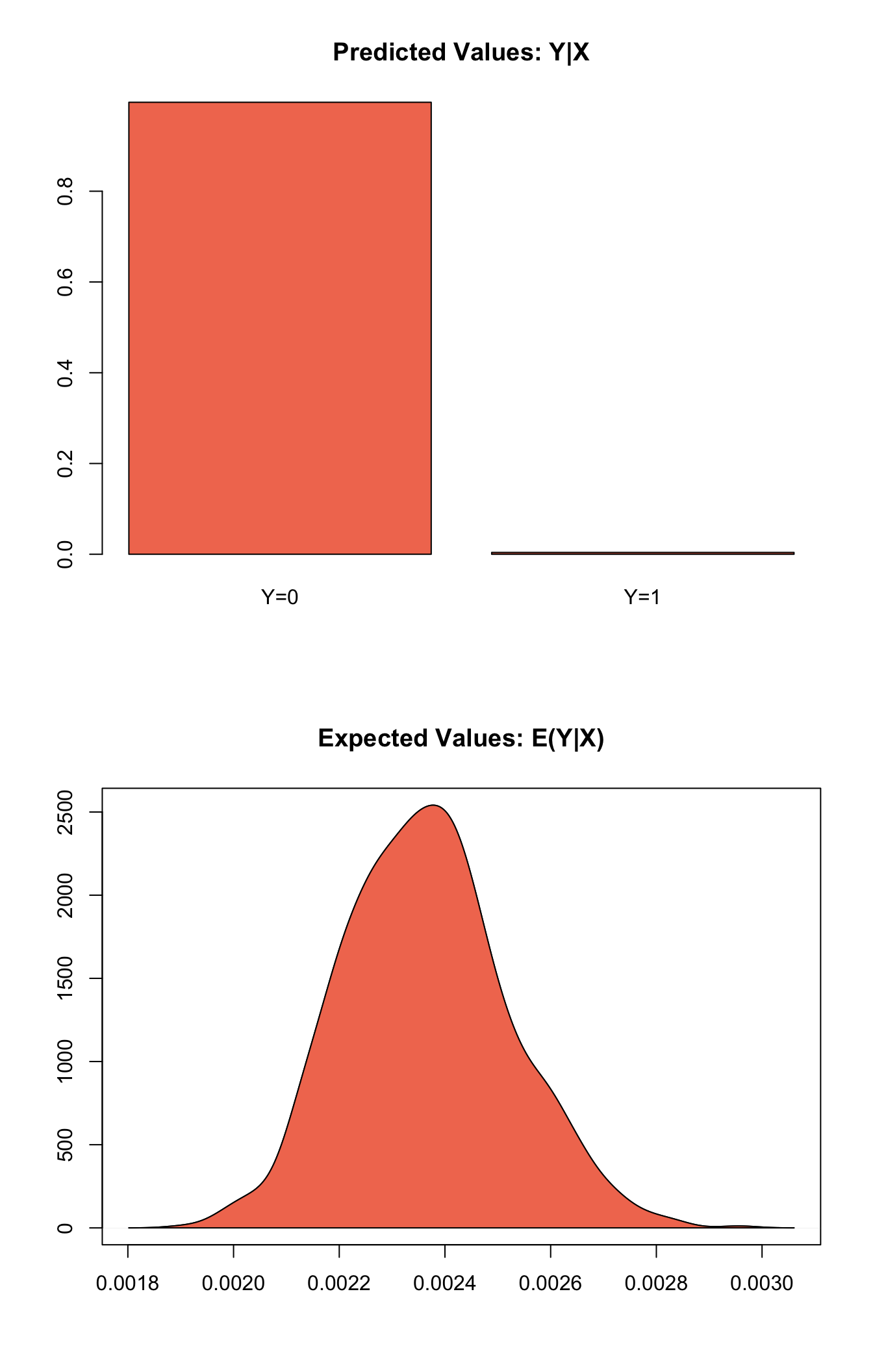
Graphs of Quantities of Interest for Rare Events Logistic Regression
Example 2: Tau with Weighting and Bias Correction
Suppose that we wish to perform case control correction using weighting (rather than the default prior correction). To estimate the model:
z.out2 <- zelig(conflict ~ major + contig + power + maxdem + mindem + years,
data = mid, model = "relogit", tau = 1042/303772,
case.control = "weighting")## How to cite this model in Zelig:
## Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau. 2017.
## relogit: Rare Events Logistic Regression for Dichotomous Dependent Variables
## in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
## "Zelig: Everyone's Statistical Software," http://zeligproject.org/Summarize the model output:
summary(z.out2)## Model:
##
## Call:
## relogit(formula = cbind(conflict, 1 - conflict) ~ major + contig +
## power + maxdem + mindem + years, data = as.data.frame(.),
## tau = 0.00343020423212146, bias.correct = TRUE, case.control = "weighting")
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.94933 -0.04958 -0.02173 0.19019 0.48253
##
## Coefficients:
## Estimate Std. Error (robust) z value Pr(>|z|)
## (Intercept) -6.61889 0.31748 -20.848 < 2e-16 ***
## major 1.67218 0.27842 6.006 1.9e-09 ***
## contig 4.01640 0.22954 17.498 < 2e-16 ***
## power 0.28836 0.41574 0.694 0.487925
## maxdem 0.06629 0.01925 3.444 0.000573 ***
## mindem -0.08143 0.02996 -2.718 0.006572 **
## years -0.11707 0.01336 -8.764 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 143.116 on 3125 degrees of freedom
## Residual deviance: 91.178 on 3119 degrees of freedom
## AIC: 27.041
##
## Number of Fisher Scoring iterations: 10Set the explanatory variables to their means:
x.out2 <- setx(z.out2)Simulate quantities of interest:
s.out2 <- sim(z.out2, x = x.out2)
summary(s.out2)## Model:
##
## Call:
## relogit(formula = cbind(conflict, 1 - conflict) ~ major + contig +
## power + maxdem + mindem + years, data = as.data.frame(.),
## tau = 0.00343020423212146, bias.correct = TRUE, case.control = "weighting")
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.94933 -0.04958 -0.02173 0.19019 0.48253
##
## Coefficients:
## Estimate Std. Error (robust) z value Pr(>|z|)
## (Intercept) -6.61889 0.31748 -20.848 < 2e-16 ***
## major 1.67218 0.27842 6.006 1.9e-09 ***
## contig 4.01640 0.22954 17.498 < 2e-16 ***
## power 0.28836 0.41574 0.694 0.487925
## maxdem 0.06629 0.01925 3.444 0.000573 ***
## mindem -0.08143 0.02996 -2.718 0.006572 **
## years -0.11707 0.01336 -8.764 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 143.116 on 3125 degrees of freedom
## Residual deviance: 91.178 on 3119 degrees of freedom
## AIC: 27.041
##
## Number of Fisher Scoring iterations: 10Model
- Like the standard logistic regression, the stochastic component for the rare events logistic regression is:
\[ Y_i \; \sim \; \textrm{Bernoulli}(\pi_i), \]
where \(Y_i\) is the binary dependent variable, and takes a value of either 0 or 1.
- The systematic component is:
\[ \pi_i \; = \; \frac{1}{1 + \exp(-x_i \beta)}. \]
-
If the sample is generated via a case-control (or choice-based) design, such as when drawing all events (or “cases”) and a sample from the non-events (or “controls”) and going backwards to collect the explanatory variables, you must correct for selecting on the dependent variable. While the slope coefficients are approximately unbiased, the constant term may be significantly biased. Zelig has two methods for case control correction:
- The “prior correction” method adjusts the intercept term. Let \(\tau\) be the true population fraction of events, \(\bar{y}\) the fraction of events in the sample, and \(\hat{\beta_0}\) the uncorrected intercept term. The corrected intercept \(\beta_0\) is:
\[ \beta = \hat{\beta_0} - \ln \left[ \bigg( \frac{1 - \tau}{\tau} \bigg) \bigg( \frac{\bar{y}}{1 - \bar{y}} \bigg) \right]. \]
- The “weighting” method performs a weighted logistic regression to correct for a case-control sampling design. Let the 1 subscript denote observations for which the dependent variable is observed as a 1, and the 0 subscript denote observations for which the dependent variable is observed as a 0. Then the vector of weights \(w_i\)
\[ \begin{aligned} w_1 &=& \frac{\tau}{\bar{y}} \\ w_0 &=& \frac{(1 - \tau)}{(1 - \bar{y})} \\ w_i &=& w_1 Y_i + w_0 (1 - Y_i) \end{aligned} \]
If \(\tau\) is unknown, you may alternatively specify an upper and lower bound for the possible range of \(\tau\). In this case, the relogit procedure uses “robust Bayesian” methods to generate a confidence interval (rather than a point estimate) for each quantity of interest. The nominal coverage of the confidence interval is at least as great as the actual coverage.
- By default, estimates of the the coefficients \(\beta\) are bias-corrected to account for finite sample or rare events bias. In addition, quantities of interest, such as predicted probabilities, are also corrected of rare-events bias. If \(\widehat{\beta}\) are the uncorrected logit coefficients and bias( \(\widehat{\beta}\)) is the bias term, the corrected coefficients \(\tilde{\beta}\) are
\[ \widehat{\beta} - \textrm{bias}(\widehat{\beta}) = \tilde{\beta} \]
The bias term is
\[ \textrm{bias}(\widehat{\beta}) = (X'WX)^{-1} X'W \xi \]
where
\[ \begin{aligned} \xi_i &=& 0.5 Q_{ii} \Big( (1 + w-1)\widehat{\pi}_i - w_1 \Big) \\ Q &=& X(X'WX)^{-1} X' \\ W = \textrm{diag}\{\widehat{\pi}_i (1 - \widehat{\pi}_i) w_i\} \end{aligned} \]
where \(w_i\) and \(w_1\) are given in the “weighting” section above.
Quantities of Interest
For either one or no \(\tau\):
The expected values (qi$ev) for the rare events logit are simulations of the predicted probability
\[ E(Y) = \pi_i = \frac{1}{1 + \exp(-x_i \beta)}, \]
given draws of \(\beta\) from its posterior.
The predicted value (qi$pr) is a draw from a binomial distribution with mean equal to the simulated \(\pi_i\).
The first difference (qi$fd) is defined as
\[ \textrm{FD} = \Pr(Y = 1 \mid x_1, \tau) - \Pr(Y = 1 \mid x, \tau). \]
- The risk ratio (qi$rr) is defined as
\[ \textrm{RR} = \Pr(Y = 1 \mid x_1, \tau) \ / \ \Pr(Y = 1 \mid x, \tau). \]
For a range of \(\tau\) defined by \([\tau_1, \tau_2]\), each of the quantities of interest are \(n \times 2\) matrices, which report the lower and upper bounds, respectively, for a confidence interval with nominal coverage at least as great as the actual coverage. At worst, these bounds are conservative estimates for the likely range for each quantity of interest. Please refer to for the specific method of calculating bounded quantities of interest.
In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is
\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - E[Y_i(t_i=0)] \right\}, \]
where \(t_i\) is a binary explanatory variable defining the treatment (\(t_i=1\)) and control (\(t_i=0\)) groups. Variation in the simulations are due to uncertainty in simulating \(E[Y_i(t_i=0)]\), the counterfactual expected value of \(Y_i\) for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to \(t_i=0\).
- In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is
\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - \widehat{Y_i(t_i=0)} \right\}, \]
where \(t_i\) is a binary explanatory variable defining the treatment (\(t_i=1\)) and control (\(t_i=0\)) groups. Variation in the simulations are due to uncertainty in simulating \(\widehat{Y_i(t_i=0)}\), the counterfactual predicted value of \(Y_i\) for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to \(t_i=0\).
Output Values
The Zelig object stores fields containing everything needed to rerun the Zelig output, and all the results and simulations as they are generated. In addition to the summary commands demonstrated above, some simply utility functions (known as getters) provide easy access to the raw fields most commonly of use for further investigation.
In the example above z.out1$get_coef() returns the estimated coefficients, z.out1$get_vcov() returns the estimated covariance matrix, and z.out1$get_predict() provides predicted values for all observations in the dataset from the analysis.
Differences with Stata Version
The Stata version of ReLogit and the R implementation differ slightly in their coefficient estimates due to differences in the matrix inversion routines implemented in R and Stata. Zelig uses orthogonal-triangular decomposition (through lm.influence()) to compute the bias term, which is more numerically stable than standard matrix calculations.